用于太赫兹到光频率快速频谱分析的1GHz单腔双光梳激光器
(本文译自(Gigahertz Single-cavity Dual-comb Laser for Rapid Time-domain Spectroscopy: from Few Terahertz to Optical Frequencies )
Benjamin Willenberg1,*,x, Christopher R. Phillips1,*, Justinas Pupeikis1 , Sandro L. Camenzind1 , Lars Liebermeister2 , Robert B. Kohlhass2 , Björn Globisch2 , and Ursula Keller1)
介绍
在这篇论文中,我们介绍了一个自由运行的单腔体空间复用的1.18 GHz固态双梳激光器激光器。可实现的高重复率差结合激光的低噪声性能,可以在太赫兹时域光谱学(TDS)应用中进行计算梳齿追踪和相干平均。我们在激光波长约为1.05微米时,通过对20厘米长、1bar气体池中C2H2(乙炔)的吸收测量,证明了这种能力。此外,激光器的0.85纳秒延迟扫描范围非常适合高分辨率太赫兹计量学,具有快速的单次跟踪更新速率。我们使用高效的光电导天线器件进行了初步实验。在太赫兹光谱测量中,我们在2秒的积分时间内达到了55 dB的峰值光谱动态范围,允许探测3 THz的吸收特征。
该论文分为以下几个部分:第一部分介绍双梳激光器及其噪声性能。第二部分演示了C2H2的TDS测量结果。第三部分讨论了ETS应用中的定时噪声和自适应采样。第四部分重点关注太赫兹-TDS和厚度测量。
正文
基于飞秒锁模激光的光学频率梳[1-3]已实现许多计量应用如光谱学和精密测距[4,5]。双光频梳[6,7]是光学频率梳的一个有趣的扩展,它包括一对脉冲有细x间的差频会产生相应的频率线,从而在易于访问的射频域中实现了对梳状线的分辨测量,双梳源也是等效时间采样(ETS)测量技术的强有力工具,有时被称为异步光学采样(ASOPS)。该技术利用两个脉冲列之间的延迟扫描,实现对信号的采样。在这个技术中,一个实时持续时间为1/frep的窗口可以被转换为一个等效时间持续时间为1/Δfrep的窗口,其中Δfrep是其中一个梳齿重复的频率,Δfrep是两个梳齿重复频率之间的差异。这相当于将时间轴按比例因子frep/Δfrep进行缩放。由于这种延迟扫描方法不需要任何移动部件,因此与传统的基于机械延迟线的泵浦探测测量相比,可以获得更快速和更长距离的扫描。高更新速率是重要的先进性能,因为它们能够实现实时材料检查和无标记成像。
基于光频梳的传感技术的一个关键参数是光源可覆盖的波长范围。许多强的光谱特征位于近红外波长范围之外,这意味着必须将已经成熟的在这一波长范围内工作的激光技术与频率转换方案相结合。例如,最近的研究使用差频发生、光参量振荡和光整流等技术,成功地扩展了可探测的波长范围,包括分子的功能团区域(3至5微米)和分子指纹区域(5至20微米)。光整流的一个特殊情况是太赫兹辐射(0.1到10 THz)的产生,由于高效光电导天线的进展,在最近几年中太赫兹辐射得到了广泛关注。
THz频段对于科学和工业应用非常重要,因为它允许对许多在可见光和红外线下不透明的材料进行非侵入式检测和分析。应用包括检测1到5 THz范围内的光谱特征,以区分外观相似的塑料和爆炸物[16]、通过不透明包装进行质量控制监测、对油漆进行微米级精度的非侵入式层厚度测量[17]、高分辨率气体光谱学、以及作为标签自由分析生物组织的X射线技术的替代方法(因为THz辐射不会产生电离效应)[18]。这些应用通常采用太赫兹时域光谱技术(THz-TDS)来解决。在THz-TDS中,一个光脉冲列在一个发射器装置上产生一列单周期的THz脉冲,而另一个光脉冲列则被延迟,并在一个接收器装置上等效时间采样THz场[19]。过去十年中,光导式天线(PCAs)的进展使它们成为桌面系统的选择,转换效率高达3.4%的功率[20],在适度的光脉冲能量下为数百皮焦耳。除了基于PCA的实验外,利用非线性晶体和≫nJ级光脉冲能量产生THz也受到了极大的关注[21,22]。
许多PCA系统使用重复频率约为100 MHz的激光与机械延迟级联以实现THz波形的等效时间采样,但这会在速度和扫描范围之间产生严重的权衡。同样类型的激光可以通过ETS(等效时间采样)实现THz-TDS,但仅特定应用需要相应的10ns的长延迟范围(例如测量具有长响应时间或低压下分子气体的尖锐吸收线的目标)10ns。对于许多应用,较短的范围(<1 ns)和相应的光谱分辨率(>1 GHz)已足够,例如在环境压力下进行气体光谱学,或检测薄膜层厚度的微小变化[23]。将扫描范围限制在较短的范围内可以避免在时间窗口结束时出现死时间,这提高了信噪比,因为有效信号将占据更大的测量窗口。为了解决这个问题,电子控制的光采样(ECOPS)[24]和其他技术[25,26]已经被开发出来,通过在小于重复频率的倒数的有限范围内电子控制脉冲之间的延迟。另一种可能更简单的方法是使用高重复频率自由运行双梳激光器。千兆赫兹的重复频率可以在全延迟范围内进行≪100 fs的分辨率扫描,并实现高(多千赫兹)更新速率。在THz-TDS中,结合PCA使用这种激光器也是提高信号强度的有前景的途径,因为使用更高的平均功率’可以同时保持在设备的脉冲能量损伤阈值以下。使用1 GHz [27]和10 GHz [28]的钛宝石激光器探测脉冲-探测谱也已经进行了研究,但是钛宝石技术的高成本阻碍了更广泛的采用。
近年来,由于高重复率钇和铒基频率梳的进展,使用千兆赫激光进行双梳光谱学和THz-TDS的应用引起了人们的新关注[29-34]。具有低损耗、低非线性、低色散腔的二极管泵浦固体激光器非常适合产生千兆赫梳[35,36],它们比传统的钛宝石系统简单得多,同时提供更好的高频泵浦强度抑制。与光纤激光器相比,它们也支持更低的噪声[31]、更高的功率,并且显示出更简单的重复频率缩放。
该文提到了在双频梳应用的实际部署中,系统复杂度是另一个关键的考虑因素。传统系统由一对锁定的飞秒激光器组成,复杂度很高,需要几个反馈环。有一种先进的替代方法是使用单腔双光梳激光器,其中通过让两个频梳共享同一个激光腔体,在自由运行状态下实现频梳之间的高相干性。这种方法已经在半导体盘式激光器[37]、自由空间双向环形激光器[38]和双向模锁光纤激光器[39]等方面得到了证明。最近,我们利用双折射多路复用[40-42]或空间复用[43,44]演示了一组自由运行固态单腔室系统,使用所有常见光学元件,具有超低的相对时序噪声性能。 [43]中报告的系统可以实现子周期相对时序抖动([20 Hz,100 kHz]积分范围),从而超越了ASOPS系统在泵浦-探测测量方面使用两个锁定激光器的性能。此外,低损耗、低非线性和低色散腔体的二极管泵浦固体激光器非常适合产生千兆赫的梳光谱。它们比传统的钛宝石系统更简单,同时还能更好地抑制高频泵浦强度的波动,支持更低噪声、更高功率,并且与光纤激光器相比重复率扩展更为简单。
双梳激光器的布局如图1(a)所示。线性共焦激光腔与单片双棱镜(179°顶角)空间复用,产生在有源元件(增益晶体和SESAM)上的分离光斑,从而减小串扰。请注意,实际的腔复用是为了对称性而在垂直方向上实现的,但为了简单起见,在图1(a)中以水平方向显示。在高反射(HR)涂层双棱镜上,光束间隔为1.6毫米,通过双棱镜的横向平移可以连续调节重复率差在[-175,175] kHz范围内。双梳激光腔的技术细节在方法部分中描述。
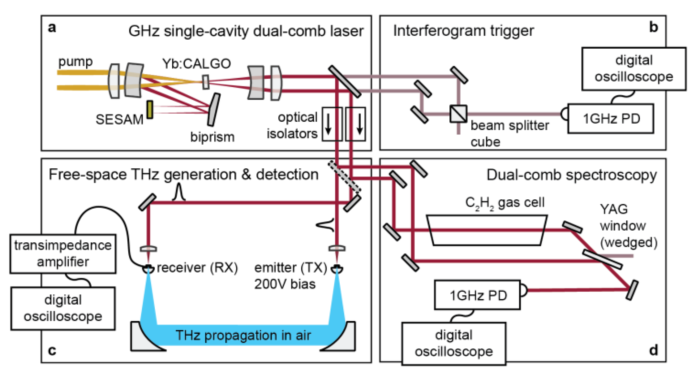
图1:示意图:(a)基于空间多路复用的双棱镜共焦腔固态SESAM模锁定GHz双梳激光器,(b)通过非偏振分束器立方体的两个梳的相干重叠触发的干涉(c)用于THz时间域光谱学的设置,其中采用高效自由空间光电导天线进行THz产生和检测(d)在乙炔(C2H2)气体室内进行的双梳光谱学分析。
两个光梳显示出同时自启动和稳健的锁模运行,其平均输出功率范围为每个梳子80毫瓦至110毫瓦,受可用泵浦功率限制。两个光梳具有几乎相同的光学特性。功率曲线是线性的,激光在最高功率操作点时达到了23%的光学转化效率(参见图2(a),随着腔内功率的增加,脉冲持续时间缩短的趋势符合孤子形成的预期逆比例规律(参见图2(a))。在最高功率操作点,脉冲的持续时间为77 fs,通过二次谐波自相关测量得到(参见图2(d)),在光谱上的半高全宽为16 nm(参见图2(b)),中心波长分别为1058 nm(comb 1)和1057 nm(comb 2)。我们观察到两个梳的无杂波射频(RF)频谱,在一个重复频率约为1.1796 GHz的频点上(图2(c))。重复率差在这里被
设置为Δfrep = 21.7 kHz。
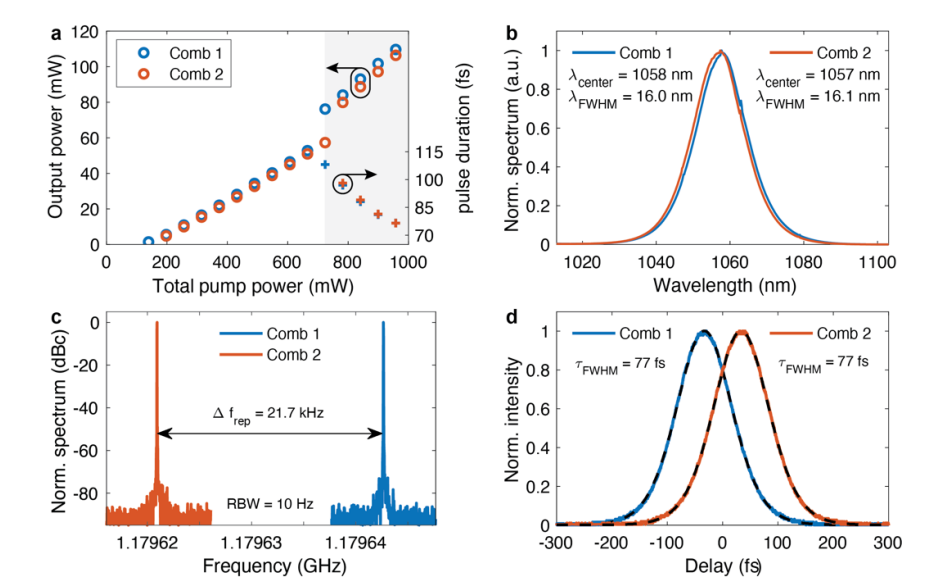
图2:双梳激光器输出特性的表征,两个梳同时运行:(a) 平均输出功率和脉冲持续时间随泵浦电流的变化。详细的锁模诊断结果显示在(b)-(d),用于后续的测量。(b) 光谱。(c) 在重复频率差为21.7 kHz时,每个梳的射频频谱。(d) 通过二次谐波自相关测量的脉冲持续时间。脉冲持续时间τFWHM是通过反卷积获得的,假设为sech2脉冲形状(虚线对应于sech2拟合)。
我们对激光的相对强度噪声(RIN)和定时抖动进行了表征。有关这些测量的详细信息在补充材料中给出。首先,我们分析了每个单独梳的RIN。在自由运行情况下,两个光梳的RMS强度噪声均为<0.01%,如图3(a,c)所示。这里,RMS强度噪声是从积分相对强度噪声(RIN)的功率谱密度(PSD)(积分范围[10 Hz,10 MHz])中获得的。通过反馈回路对泵浦功率进行主动稳定,可以获得更低的RIN。在泵浦稳定情况下(实现细节见方法),我们在高达100 kHz的频率范围内获得了15 dB的RIN抑制,从而使积分RMS强度噪声(图3(a,c))降低了一倍,接近我们最近报告的多模泵浦80 MHz激光器[43]的3.1 x 10-5[1 Hz, 1 MHz]的超低值。这样的RIN水平有利于泵浦探测研究,例如皮秒超声和时间域热反射分析[45]。
图3(b,d)展示了各个频梳的相位噪声。在2 kHz到100 kHz的频率范围内,时序抖动功率谱密度(PSD)相对平稳地随频率下降。当应用泵浦反馈时,该频段噪声均匀抑制约10 dB,这表明该频段的噪声对应于泵浦的RIN。在泵浦RIN稳定和自由运行情况下,积分时间抖动分别为2.4 fs和6.4 fs(积分范围[2 kHz,1 MHz])。在低于2 kHz的较低频率下,抖动不再由RIN主导,而是由机械噪声源引起的,这符合我们的非优化光学板实现的腔体预期。
任何双梳源的相干平均应用中至关重要的一项参数是两个梳之间Δfrep的相对时间或相位噪声。在图3(b,d)中标有“不相关"的曲线中显示了此量,该量是通过[46]中提出的方法确定的。这个量的重要性在于:(i) 它通过frep/Δfrep的比率决定了在等效时间采样应用中的时序轴稳定性,(ii) 是相干双梳光谱中涉及射频梳线路中噪声的主要贡献因素,以及 (iii) 揭示了共腔结构抑制噪声的程度。我们的无相关噪声的测量结果表明,机械噪声源(在频率<2 kHz,单个frep测量中可见)被强烈抑制。在自由运行配置(无泵浦反馈)中,高频噪声也被抑制,导致全频段高达约20 dB的公共噪声抑制(达到测量的噪声基底),除了系统中一个大约在450 Hz左右的反相关机械谐振。> 2 kHz分量的抑制是因为两个梳共享泵浦激光。
有趣的是,尽管反馈强烈抑制了单个梳齿的抖动,但泵浦反馈并没有显着改变不相关噪声。对于积分范围[2 kHz,1 MHz],双梳激光器的两种操作模式都产生小于1 fs的不相关时序抖动。泵浦RIN稳定未能影响不相关噪声的可能解释是存在非对称噪声贡献,例如来自泵浦的非理想偏振消光比。尽管如此,带有和不带有泵浦反馈的噪声水平对于本文第2和第4节中讨论的应用演示已经足够低。因此,为了简单起见,我们在后续测量中将激光器设置为自由运行模式。
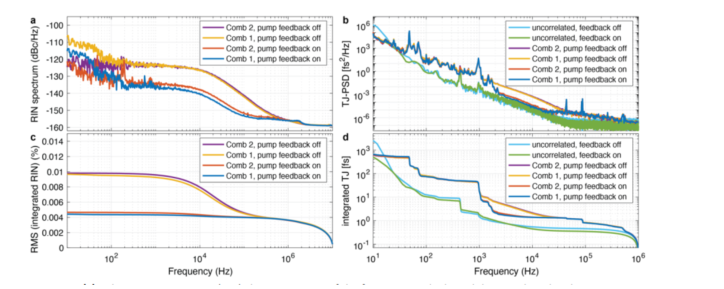
图3:(a)自由运行的双梳激光器在泵浦强度稳定和非稳定情况下的相对强度噪声(RIN)特性(详见补充材料),以及RIN的RMS积分值(c)。两个梳子同时以激光器的最大输出功率约为110 mW/梳子的功率运行。(b)相应的时序抖动(TJ)特性:单侧功率谱密度(PSD)和积分时序抖动量(d)由参考文献[46]测量两个单独光梳和不相关噪声的单侧功率谱密度(PSD)和积分时序抖动量(d),测量方法见参考文献[46]。
基于其超低噪声性能,自由运行的双频激光器可以直接用于双频激光光谱仪(DCS)。然而,由于时序和其他波动的影响,两个激光梳之间的混频拍在干涉图形上形成时无法直接进行相干平均,需要使用相位校正程序。这种相位校正的可行性可以通过跟踪干涉图的载波包络相位
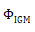
进行评估[44]。我们选用重复频率相对较高的值Δfrep
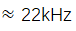
来有效降低低频(<2kHz)技术噪声源的影响。干涉图是通过将两个共极化梳齿交叉在一个非偏振分束器立方体上获得的,如图1(b)所示。图4(a)展示了一个典型的示例,展示了干涉图相位的二阶有限差分
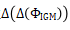
的时间演化。由于波动不断地被界定在之间,因此可以在时间上明确无误地展开相位
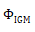
[44]。在补充材料中,我们更详细地描述了在使用不同的Δfrep值时对所呈现的激光进行相位校正的可行性。
为了确认该光源适用于类似 DCS 的相位敏感应用,我们展示了乙炔在 1040 纳米附近的转动振动带的光谱。该设置如图1(d)所示:其中一个输出光梳经过一个填有乙炔(1 bar,室温.)的 20 厘米长参考气体池。将该光与第二个光梳在倾斜的 YAG 窗口上以约 70° 的入射角度下进行 S 偏振的合并,组合后的端口每个单独的光梳初始强度约为 40%,同时避免在检测路径中出现任何谐振腔效应或脉冲重复。来自组合端口的光被衰减并进行光纤耦合,然后在快速光电二极管(Thorlabs,DET08CFC)上检测两个光梳的拍频信号,该光电二极管处于其线性响应区域。
为了以组合线分辨率提取气体靶的光谱信息,我们采用[44]的方法:将干涉图周期进行相位校正,通过用组合因子Δfrep/frep缩放时间轴并相加将其转移到光学域。将这个相干平均信号的傅里叶变换与频移相结合,可以在光学频率域内获得组合线分辨率的光谱信息。双梳激光器的重复频率frep确定了单个光学组合线之间的间距。图4(b)显示了乙炔气体池在0.8秒积分时间测量下的透射光谱,并与HITRAN数据[47]的预测进行了比较。测量和计算出的光谱在整个乙炔吸收在1040 nm附近的(转动-振动)分支处都有很好的一致性。请注意,为了获得更好的信噪比,可以将激光的光谱滤波至感兴趣的区域,并将相应的更高功率的光在相关的光学频率上发送到光电二极管上。在这里,我们为了简单起见使用了激光器输出提供的全光谱。
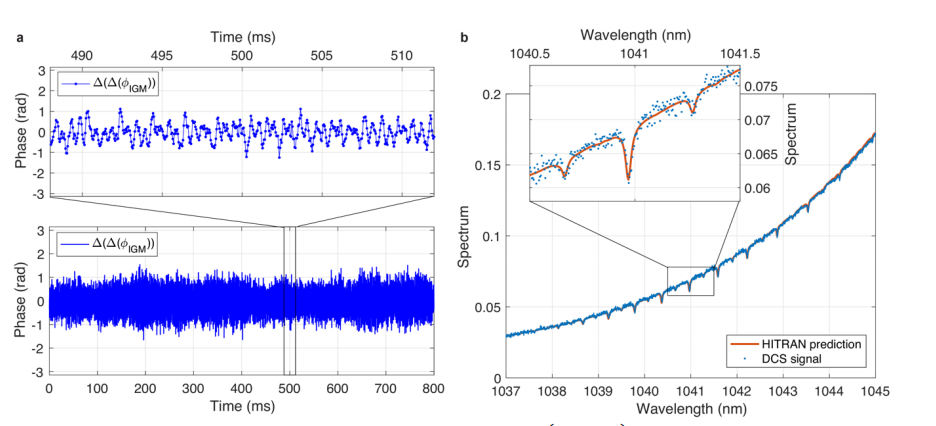
图4:(a)以重复频率差Δfrep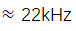 采样的干涉图相位
采样的干涉图相位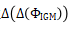 的二阶有限差分
的二阶有限差分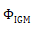 的时间演化,并放大时间轴。放大版本中的点表示单个干涉图。(b)在积分时间为0.8秒的自由运行GHz单腔双频激光器上进行的乙炔双腔光谱测量(DCS)。请注意,来自乙炔的吸收特征仅与激光器的光学光谱远翼重叠,中心波长为1057 nm。围绕1041 nm的吸收线的放大显示了DCS测量的光谱分辨率,其中每个点对应于频率间隔为frep= 1.179 GHz或约4.3 pm的单个光学腔线。
的时间演化,并放大时间轴。放大版本中的点表示单个干涉图。(b)在积分时间为0.8秒的自由运行GHz单腔双频激光器上进行的乙炔双腔光谱测量(DCS)。请注意,来自乙炔的吸收特征仅与激光器的光学光谱远翼重叠,中心波长为1057 nm。围绕1041 nm的吸收线的放大显示了DCS测量的光谱分辨率,其中每个点对应于频率间隔为frep= 1.179 GHz或约4.3 pm的单个光学腔线。
3.ETS应用中的时间噪声与自适应采样
在等效时间采样测量中,通常会使用触发信号以避免在较长时间尺度上积累时序抖动。zui小化此类时序抖动非常重要,因为它会在平均过程中模糊时间轴,因此降低信号强度和频谱分辨率。在这里,我们使用双腔干涉图(IGM)来连续跟踪和纠正自由运行激光器的时序漂移。如上所述,IGM是通过两个激光腔之间的拍频产生的(见图1(b))。每当两个激光腔的脉冲在时间上重叠时,就会出现IGM峰。为了确定这些峰的定时,我们使用希尔伯特变换的幅度提取IGM包络,然后通过进行二阶矩计算来计算时间峰位置。所得到的IGM峰时间可以在等效时间采样测量的背景下解释为延迟为零。通过在这些峰之间线性插值,我们可以在测量期间的所有时间获取两个脉冲列之间的光延迟。
通过后续IGM峰之间的时间波动(对应于周期抖动),可以分析所获得的光延迟轴的准确性。尽管可以通过IGM峰获得此抖动(这是我们用于自适应采样的THz-TDS测量本身的方法),但通过[46]的方法获得PN-PSD的相位噪声功率谱密度可以获得更多关于激光器时间特性的信息,如图3(b)所示。
通过 PN-PSD 的加权积分是得到周期抖动的一般方法。对于一个由相位 Φ(t) 描述的信号和对应的单侧相位噪声功率谱密度 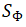 ,周期抖动可以表示为 [48]中给出公式:
,周期抖动可以表示为 [48]中给出公式:
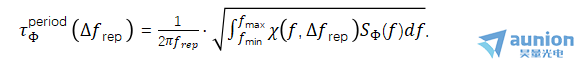
其中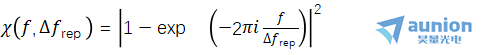 是采样频率 Δf 相关的加权因子,fmin 和 fmax 是 PN-PSD 中偏移频率 f 的积分限。
是采样频率 Δf 相关的加权因子,fmin 和 fmax 是 PN-PSD 中偏移频率 f 的积分限。
在ETS的背景下,相位Φ(t)通过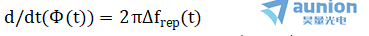 与时变重复频率差联系在一起,并且标称周期由
与时变重复频率差联系在一起,并且标称周期由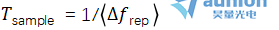 给出,其中
给出,其中 表示平均重复频率差。然而,在这种情况下,周期抖动可能会具有误导性,因为它受到缓慢漂移的影响,即使自适应采样也会纠正这些漂移。为解决这个问题,我们确定自适应采样无法纠正的周期抖动部分。由于混叠效应,高于Δfrep的高频噪声部分被部分投影到低于Δfrep的频率上,这是TJ-PSD在这些频率上仍存在有限贡献的原因。
表示平均重复频率差。然而,在这种情况下,周期抖动可能会具有误导性,因为它受到缓慢漂移的影响,即使自适应采样也会纠正这些漂移。为解决这个问题,我们确定自适应采样无法纠正的周期抖动部分。由于混叠效应,高于Δfrep的高频噪声部分被部分投影到低于Δfrep的频率上,这是TJ-PSD在这些频率上仍存在有限贡献的原因。
与其为每个重复频率差Δfrep设置执行实验,我们可以根据参考文献[44,46]直接从击拍测量获得的相位Φ(t)中提取信息。为了模拟自适应采样步骤,我们计算了校正相位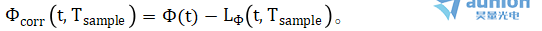
其中是 在网格点
在网格点 之间的连续相位Φ的线性插值。在图5(a)中,显示了不相关的时间抖动功率谱密度以及模拟重复频率差为1 kHz、5 kHz和22 kHz时对应的自适应采样校正的功率谱密度。对于不同的采样频率
之间的连续相位Φ的线性插值。在图5(a)中,显示了不相关的时间抖动功率谱密度以及模拟重复频率差为1 kHz、5 kHz和22 kHz时对应的自适应采样校正的功率谱密度。对于不同的采样频率 应用周期抖动形式化方法会得到
应用周期抖动形式化方法会得到 图5(b)呈现的曲线。对于自由运行的双梳激光器,我们发现在重复频率失谐Δfrep>18 kHz时,经过自适应采样后光学延迟轴的RMS时间误差低于1 fs,在重复频率失谐Δfrep>1 kHz时低于10 fs。需要注意的是,在1 kHz以下的技术噪声可以在机械优化的系统中得到缓解,因为当前的设置是在一个光学面包板上使用标准的反射镜支架和5厘米高的支撑柱搭建的。在下面讨论的THz-TDS应用演示中,我们以两种配置运行双梳激光器:在Δfrep= 22 kHz时,这些技术噪声源可以忽略不计,而在Δfrep = 1 kHz时,自适应采样周期抖动值10 fs仍然比预期的zui快时间特征>200 fs(考虑到zui大THz频率为5 THz)要小得多。
图5(b)呈现的曲线。对于自由运行的双梳激光器,我们发现在重复频率失谐Δfrep>18 kHz时,经过自适应采样后光学延迟轴的RMS时间误差低于1 fs,在重复频率失谐Δfrep>1 kHz时低于10 fs。需要注意的是,在1 kHz以下的技术噪声可以在机械优化的系统中得到缓解,因为当前的设置是在一个光学面包板上使用标准的反射镜支架和5厘米高的支撑柱搭建的。在下面讨论的THz-TDS应用演示中,我们以两种配置运行双梳激光器:在Δfrep= 22 kHz时,这些技术噪声源可以忽略不计,而在Δfrep = 1 kHz时,自适应采样周期抖动值10 fs仍然比预期的zui快时间特征>200 fs(考虑到zui大THz频率为5 THz)要小得多。
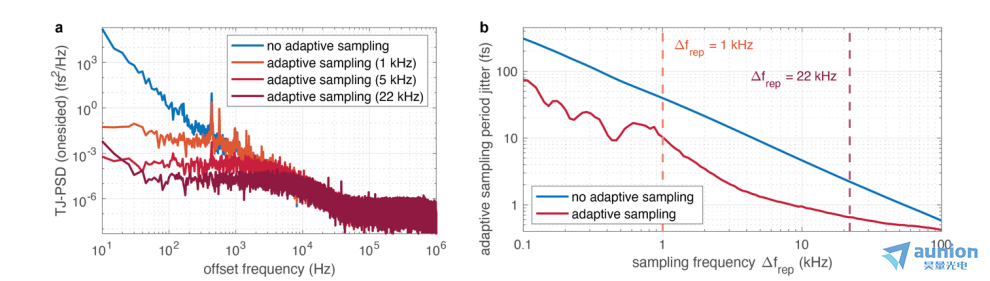
图5:(a)不相关自由运行双梳的时间抖动功率谱密度(TJ-PSD)在不同自适应采样条件下的情况。显示了三种不同的自适应采样情况(对应于Δfrep值为1 kHz、5 kHz和22 kHz)。 (b)在不同采样频率(即重复频率差Δfrep的设置)下自适应采样后光学延迟轴的周期抖动,用于自由运行双梳激光器。
4. 太赫兹时域光谱学
在太赫兹实验中,我们将两个梳的光直接引导到两个自由空间光电导天线上(图1(c))。在发射器器件的有源区域内,每个激光脉冲会产生一个局部电荷云,该电荷云在两个电极之间的50微米间隙中受到偏置电场(40 kV/cm)的加速,从而产生脉冲太赫兹辐射。所使用的掺铁InGaAs材料平台的超快捕获时间使得太赫兹脉冲的频率范围高达>6 THz [49]。
在THz实验中,我们将两个梳的光线直接照射到两个自由空间光电导天线上(图1(c))。在发射器器件的活动区域内,每个激光脉冲会生成一个局部电荷云,通过偏置电场(40 kV/cm)在两电极之间的50 µm间隙中加速并产生脉冲THz辐射。铁掺杂InGaAs材料平台的超快俘获时间使得产生具有高达>6 THz频率内容的短THz脉冲成为可能[49]。
产生的THz辐射通过一对硅球透镜(直接安装在光电导天线上)和金属偏离轴抛物面镜进行聚焦并重新聚焦到接收器器件上。在接收器器件中,第二个梳的光脉冲作为门用于光电子采样THz波。更具体地说,每个光脉冲在10 µm的天线间隙中生成一个电荷云,被THz波的电场加速,从而在nA-µA范围内引起小电流,被转移阻抗放大并检测在示波器上。
为了确保THz光电导天线和激光振荡器之间没有光学反馈,两个自由空间光路都包括法拉第隔离器(EOT,PAVOS +)。发射和接收臂中的光功率由一对半波片和偏振分束器控制。光束在发射器上被聚焦到亚50 µm的斑点(1/e2直径),用f=50 mm的非球面透镜,在接收器上聚焦到亚10 µm的斑点,用f=20 mm的透镜。由于透明光学元件和隔离器晶体的正色散,加上由啁啾镜提供的负色散(总计约为-4000 fs^2),以确保在光电导器件上压缩77 fs脉冲。为了进行平均处理,我们使用IGM信号(在第3节中描述)实现THz时间迹线的自适应采样,并使用光学延迟轴的线性插值。2秒积分或约44000次平均的结果如图6所示。主要的THz峰在零光学延迟处重复出现,其重复频率为1/Δfrep≈850 ps(标志着扫描窗口的末端),然后是由自由空间THz光束路径中水蒸气自由感应衰减引起的振荡,其长度约为30 cm。通过傅里叶变换得到的频谱域中,吸收特征更加清晰可见,使用500 ps的缩窄窗口进行调制。我们使用这个缩窄窗口来抑制关于光学延迟为600 ps的THz时间迹线上的特征,这个特征在第4.2节中进行了更详细的讨论。减少的光学延迟导致THz频谱中的频谱分辨率为2 GHz。在这些条件下,我们在THz功率谱密度中发现35 dB的峰动态范围,可以解决高达3 THz的光学频率吸收特征(图6(c))。噪声水平是通过对仅将接收器装置照明而不产生THz辐射的单独时间迹线进行确定的。背景迹线的处理与信号迹线的处理相同,但在频率域中进行zui终的平滑处理,采用移动平均方法。
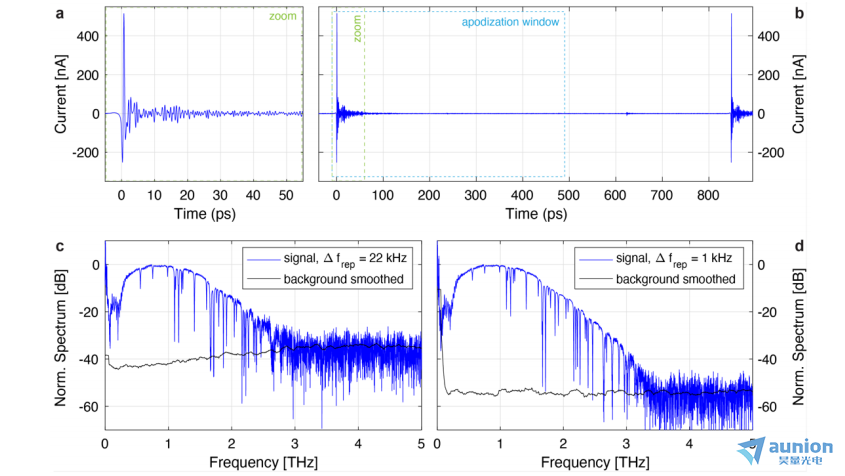
图6:(a) THz信号时间迹线的前50 ps的放大图(b),得自对双脉冲激光的重复频率差为~22 kHz的全光学延迟范围1/Δfrep = 850 ps的2秒积分时间或约44k次平均值。发射器施加的偏压为200 V,到达发射机和接收机的平均光功率分别为80 mW和30 mW。注意,应用了数字带通滤波器,将信号限制在THz频率范围内[50 GHz,5 THz]。前50 ps延迟范围表明自由空间THz光束路径中的吸收导致了明显的自由感应衰减。(c)由(b)通过傅里叶变换和500 ps调制窗口得到的THz信号功率谱密度,得到2 GHz的频谱分辨率和35 dB的动态范围。(d)通过改善放大器噪声,以更低的更新速率Δfrep = 1 kHz,在2秒积分时间内获得了动态范围增加到55 dB的THz谱。在两种情况下,平滑背景是从相应的分离时间迹线中获得的,在这些时间迹线中,自由空间THz光束路径被阻断。明显的吸收特征来自空气路径中水的吸收。请注意,由于两次测量的不同湿度条件((c)为晚夏,(d)为初冬),吸收强度发生了变化。
在这种高更新速率(Δfrep ≈22 kHz)下获得的THz频谱动态范围很大程度上受到转阻放大器的噪声系数的限制。使用高重复率差操作激光需要足够的射频(RF)检测带宽来读取接收器设备的输出。光学THz频率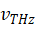 根据等效时间缩放因子Δfrep/frep映射到RF频率范围内。
根据等效时间缩放因子Δfrep/frep映射到RF频率范围内。
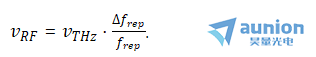
为了探测高达5 THz的THz频率,需要93 MHz的射频带宽。用高增益带宽低噪声的放大器放大弱信号是有挑战性的。在我们的检测方案中,我们使用一个3 dB带宽为200 MHz,传输增益为104 V/A的转移阻抗放大器(Femto HCA-S),然后是一个带宽宽的低噪声电压放大器(Femto DUPVA-1-70),其电压增益为30 dB。zui后,在数字化之前,我们使用一个200 MHz的抗混叠滤波器(Minicircuits BLP-200+)和示波器(Lecroy WavePro 254HD)。关于这些条件下获得的动态范围的详细讨论在第4.1节中提供。为了证明放大器对动态范围的限制,我们进行了额外的测量,更新速率为1 kHz,因此对射频检测带宽的要求放松到约4.2 MHz(对于高达5 THz的THz频率)。同时,自由运行的双频激光器的低噪声性能和自适应采样步骤导致周期抖动小于10 fs(第3节)。为了确保频率<5 THz的光谱信息不会在时间轨迹的后续平均步骤中被清除,我们使用DHPCA-100放大器(FEMTO)替换了HCA-S放大器(传输阻抗增益105 V/A,输入等效噪声电流480 fA/√Hz,射频带宽3.5 MHz),结果使得THz信号的PSD的信噪比提高了20 dB(图6(d))。对于两种配置(Δfrep≈22 kHz和Δfrep≈1 kHz),THz谱都显示出相同的尖锐吸收峰,可以被识别为水吸收。图7显示了这些吸收峰在Δfrep=1 kHz的情况下与HITRAN预测[47]的比较。测量位置和吸收峰的相对强度与HITRAN预测的非常好的一致性表明,在我们的自由运行双梳THz测量中,光延迟轴经过了良好的校准和线性化。
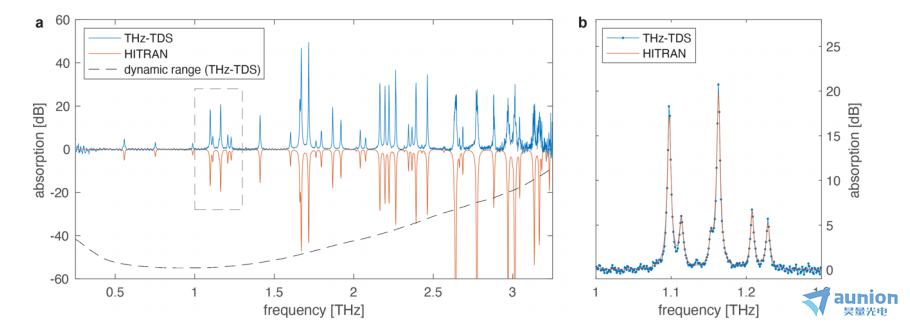
图7:(a)比较通过THz-TDS测量的约30厘米自由空间路径的吸收特征和HITRAN预测的水(H2O)蒸汽浓度为1.1%的吸收谱。 THz-TDS吸收谱是通过减去THz频谱包络(详见附录)从透射谱(图6(d))中获得的。吸收峰的位置非常吻合。对于高频率,当预测的峰吸收强度超出THz-TDS测量的动态范围时,吸收强度会有所偏差。(b)缩放到1 THz和1.3 THz之间的区域,以说明THz-TDS测量的约1.2 GHz的光谱分辨率可以很好地采样每个吸收峰。 THz-TDS测量是在重复频率差异 Δfrep= 1 kHz下进行的,总积分时间为2 s。
4.1.讨论THz-TDS测量中的动态范围
在考虑信号强度、光延迟范围和积分时间时,参考文献中的数值非常重要。在我们的实验中使用的设备,进行了参考测量,使用了驱动波长为1550 nm和脉冲重复频率为80 MHz的激光器。在这些测试条件下,获得的峰值THz信号电流强度为500-700 nA,光学功率为20 mW(发射器和接收器均为此值)。在这里,我们使用Yb激光技术探究这些掺铁PCA器件的运行情况。尽管配置大不相同(1050 nm波长和1.2 GHz重复频率),但我们获得了相似的THz信号电流(515-550 nA)。发射器上的平均光功率为80 mW,接收器上为30 mW,对应的脉冲能量远低于光电导器件的脉冲能量损伤阈值,这是由于激光的高GHz重复频率,与80 MHz的脉冲重复频率的测试测量相比。我们实验中所需的增加光功率,可以通过1550 nm和1050 nm驱动器之间的光子数缩放来解释。
虽然我们的信号强度与参考测量值相当,但我们获得了显著较低的动态范围。一篇类似的光电发射机和接收机对的THz功率谱报道了105 dB的高动态范围,该谱通过光延迟60 ps和总积分时间60 s的机械延迟扫描获得[50]。相比之下,我们在Δfrep≈ 22 kHz配置下获得了35 dB的动态范围,而在Δfrep≈ 1 kHz配置下获得了55 dB的动态范围。这种差异可以部分地解释为平均值的数量。我们扫描了更长的延迟范围,这降低了动态范围(DR)。为了比较我们的结果,请注意,THz-TDS测量的DR随着测量积分时间Tmeas和时间光延迟范围Trange缩放,对于我们的平滑窗,Trange= 500 ps,因此具有2秒示波器跟踪的有效测量时间为2 s⋅500/850 = 1.18 s。因此,(Tmeas/T2range)大约要小3530倍(35.5 dB)。
部分的误差可以通过测量的电子底噪来解释,这与所使用的跨阻放大器有关。基于机械延迟线的系统涉及到光延迟的较慢扫描,将检测到的射频频率限制在几十kHz以内。在这些条件下,低噪声跨阻放大器的输入等效噪声电流可以低至43 fA/√Hz,跨阻增益为107 V/A,而在Δfrep=22 kHz的测量中,相应的噪声电流为4900 fA/√Hz。动态范围的影响可以通过噪声水平的平方比例来获得,对于22 kHz的配置,这对应于(4900/43)2≈40 dB。考虑到这个电子因素和时间缩放因子,我们报告的35 dB的动态范围在参考文献[50]中使用的条件下应该理论上缩放到35 dB+40 dB+35.5 dB=110.5 dB。对于Δfrep=1 kHz的配置,实验采用的跨阻放大器具有10倍更低的输入等效噪声电流(480 fA/√Hz),这产生了预期的20 dB提高THz功率谱密度(Figs. 6 (c,d))。对于这种配置,我们得到类似的缩放,从测量中得到55 dB的动态范围,35 dB的时间缩放因子,以及(4900/480)2=21 dB的放大器。虽然这些计算解释了主要影响,但应注意,动态范围也可能受到接收天线本身的限制,因此进一步改进放大器必须在实验中进行测试。
4.2.THz脉冲反射和高精度厚度测量
接下来,我们展示了THz前端测量样品在自由空间THz光路中插入的光学和物理厚度的能力。在这里,我们将一块(2.0±0.2)mm厚的c切割蓝宝石窗口插入光路中。图8显示了单次延迟扫描的THz时间跟踪图与光学延迟的关系,在激光器设置的重复率差Δfrep为1 kHz时更新率为1 kHz,经过2秒的平均处理后,包括有和没有额外蓝宝石窗口的情况。请注意,时间零点对于两种情况都没有改变,并由红外的干涉信号触发确定。这使我们能够识别主THz脉冲的延迟τ1到τ3,包括蓝宝石窗口在零光学延迟周围的分镜效应(如图8(b)所示)。此外,我们可以确定在光学延迟约为600 ps处的延迟τ4到τ6,它对应于THz脉冲在总共三次而不是一次(如图8(c)所示)的发射器和接收器之间的自由空间区域传播。这是因为少量的THz光被接收器反射回自由空间路径,传播回发射器,再次反射向接收器。从窗口的光学和物理厚度对观察到的不同延迟的贡献总结在表1中。我们通过大似然拟合物理模型,发现蓝宝石窗口的物理厚度l=(2.094±0.007)mm和光学频率约为1 THz时的群组折射率ng=3.109±0.010。所述误差对应于拟合的1σ误差。两个值都与窗口的机械厚度公差和文献报道的群组折射率相符。
此外,自洽拟合结果几乎没有不确定性,证实了没有蓝宝石窗口的原始THz时间跟踪中在约600 ps光延迟处的伪影来自于THz波形在THz自由空间路径上的接收器和发射器器件上的反射。
表1:将蓝宝石窗口插入自由空间THz光束路径中导致THz波形光延迟的贡献。ng表示蓝宝石在其c轴上的群折射率,L表示窗口的物理厚度,c表示真空光速。
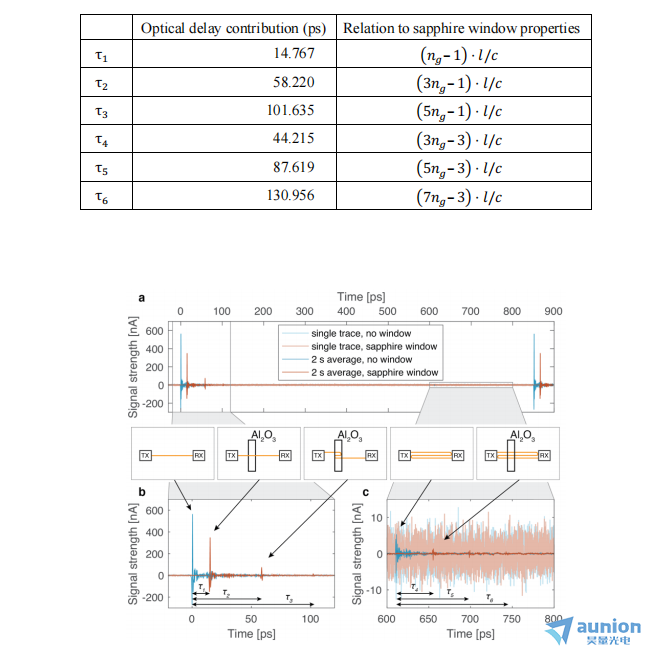
图8:测量2mm的C切割蓝宝石窗口的物理厚度和群组折射率。窗口相对于红外干涉图和空气间隙的波纹反射提供了THz波形的光延迟(见示意图)。强反射在每个光延迟扫描的时间跟踪中清晰可见,该扫描的更新率为1 kHz(a)。在(b)和(c)中指示的延迟τ1到τ6的值在表1中提供。请注意,对于延迟范围600ps到750ps,(c)中的信号轴进行了比例尺变化,以增加仅在平均后才与噪声信号分辨出来的相应信号的可见性。对于所有跟踪,已应用数字带通滤波器,将信号限制在[50 GHz,3 THz]的THz频率范围内。
讨论
我们展示了以GHz重复频率泵浦的空间多路复用单腔双光梳激光器,其受到空间单模二极管的激励。共聚焦腔设计与在反射配置下操作的双棱镜允许重复频率差异宽泛可调,达到±175 kHz,脉冲持续时间为77 fs,每个光梳激光器的平均功率为110 mW。超低噪声性能使得计算定位自由运行的激光器梳齿线输出成为可能,这反过来又使得协同平均双光梳光谱学具有接近1 GHz的谱分辨率。我们通过对乙炔气体池的原理性光谱学实验展示了这些功能,可以在1040 nm周围解决所有转动振动吸收特征,与HITRAN的预测一致。
此外,我们直接应用双光梳激光器输出进行高效的时域THz实验,探测标准空气的光谱特征,直到3 THz的频率,并在蓝宝石窗口上进行精确的层厚度测量。THz实验从全0.85 ns延迟扫描的多kHz更新速率中获益。我们的结果表明,针对1550 nm的操作设计区的掺铁InGaAs基光电天线可以通过GHz重频的1050 nm激光驱动达到zui先jin的信号强度。我们获得的55 dB动态范围可以很好地解释为THz信号强度(与兆赫级1550 nm激光器的参考测量相当)、长延迟扫描范围(0.85 ns)以及电子放大器的噪声。此外,与在约100 MHz重复频率下运行的传统系统相比,GHz重复频率下降低的脉冲能量允许更高的平均功率运行。因此,考虑到重复频率可扩展性达到10 GHz [32]以及使用功率可扩展的Yb掺杂增益介质[44],我们预计这种高性能THz-TDS实验的低复杂度单腔固态双梳激光平台,特别是在考虑到重复频率可扩展性的情况下,将会有显著的益处。
关于昊量光电:
上海昊量光电设备有限公司是光电产品专业代理商,产品包括各类激光器、光电调制器、光学测量设备、光学元件等,涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等;可为客户提供完整的设备安装,培训,硬件开发,软件开发,系统集成等服务。
References
1. H. R. Telle, G. Steinmeyer, A. E. Dunlop, J. Stenger, D. H. Sutter, and U. Keller, "carrier-envelope offset phase control: A novel concept for absolute optical frequency measurement and ultrashort pulse generation,"Appl. Phys. B 69, 327–332 (1999).
2. A. Apolonski, A. Poppe, G. Tempea, Ch. Spielmann, Th. Udem, R. Holzwarth, T. W. Hänsch, and F. Krausz,"Controlling the Phase Evolution of Few-Cycle Light Pulses," Phys. Rev. Lett. 85, 740–743 (2000).
3. D. J. Jones, S. A. Diddams, J. K. Ranka, A. Stentz, R. S. Windeler, J. L. Hall, and S. T. Cundiff, "CarrierEnvelope Phase Control of Femtosecond mode-locked lasers and Direct Optical Frequency Synthesis,"Science 288, 635–639 (2000).
4. T. Fortier and E. Baumann, "20 years of developments in optical frequency comb technology andapplications," Commun. Phys. 2, 1–16 (2019).
5. N. Picqué and T. W. Hänsch, "Frequency comb spectroscopy," Nat. Photonics 13, 146–157 (2019).
6. S. Schiller, "Spectrometry with frequency combs," Opt. Lett. 27, 766–768 (2002).
7. I. Coddington, N. Newbury, and W. Swann, "Dual-comb spectroscopy," Optica 3, 414–426 (2016).
8. K. J. Weingarten, M. J. W. Rodwel, and D. M. Bloom, "Picosecond optical sampling of GaAs integrated circuits," IEEE J. Quantum Electron. 24, 198–220 (1988).
9. P. A. Elzinga, R. J. Kneisler, F. E. Lytle, Y. Jiang, G. B. King, and N. M. Laurendeau, "Pump/probe methodfor fast analysis of visible spectral signatures utilizing asynchronous optical sampling," Appl. Opt. 26, 4303–4309 (1987).
10. N. Hoghooghi, S. Xing, P. Chang, D. Lesko, A. Lind, G. Rieker, and S. Diddams, "Broadband 1-GHz mid nfrared frequency comb," Light Sci. Appl. 11, 264 (2022).
11. O. Kara, L. Maidment, T. Gardiner, P. G. Schunemann, and D. T. Reid, "Dual-comb spectroscopy in the spectral fingerprint region using OPGaP optical parametric oscillators," Opt. Express 25, 32713–32721(2017).
12. C. P. Bauer, S. L. Camenzind, J. Pupeikis, B. Willenberg, C. R. Phillips, and U. Keller, "Dual-comb optical parametric oscillator in the mid-infrared based on a single free-running cavity," Opt. Express 30, 19904–19921 (2022).
13. S. Vasilyev, A. muraviev, D. Konnov, M. Mirov, V. Smoslki, I. Moskalev, S. Mirov, and K. Vodopyanov,
"Video-rate broadband longwave IR dual-comb spectroscopy with 240,000 comb-mode resolved datapoints," arXiv:2210.07421 (2022).
14. D. R. Bacon, J. Madéo, and K. M. Dani, "Photoconductive emitters for pulsed terahertz generation," J. Opt.
23, 064001 (2021).
15. Naftaly, Vieweg, and Deninger, "Industrial Applications of Terahertz Sensing: State of Play," Sensors 19,4203 (2019).
16. A. G. Davies, A. D. Burnett, W. Fan, E. H. Linfield, and J. E. Cunningham, "Terahertz spectroscopy ofexplosives and drugs," Mater. Today 11, 18–26 (2008).
17. M. Yahyapour, A. Jahn, K. Dutzi, T. Puppe, P. Leisching, B. Schmauss, N. Vieweg, and A. Deninger, "FastestThickness Measurements with a Terahertz Time-Domain System Based on Electronically Control LED Optical Sampling," Appl. Sci. 9, 1283 (2019).
18. E. Pickwell and V. P. Wallace, "Biomedical applications of terahertz technology," J. Phys. Appl. Phys. 39,R301–R310 (2006).
19. M. van Exter, C. Fattinger, and D. Grischkowsky, "Terahertz time-domain spectroscopy of water vapor,"Opt. Lett. 14, 1128–1130 (1989).
20. R. B. Kohlhaas, S. Breuer, L. Liebermeister, S. Nellen, M. Deumer, M. Schell, M. P. Semtsiv, W. T.Masselink, and B. Globisch, "637 μW emitted terahertz power from photoconductive antennas based on rhodium doped InGaAs," Appl. Phys. Lett. 117, 131105 (2020).
21. U. Puc, T. Bach, P. Günter, M. Zgonik, and M. Jazbinsek, "Ultra-Broadband and High-Dynamic-Range THz Time-Domain Spectroscopy System Based on Organic Crystal Emitter and Detector in transmission and Reflection Geometry," Adv. Photonics Res. 2, 2000098 (2021).
22. S. Mansourzadeh, T. Vogel, A. Omar, M. Shalaby, M. Cinchetti, and C. J. Saraceno, "Broadband THz-TDS with 5.6 mW average power at 540 kHz using organic crystal BNA," (2022).
23. D. Saeedkia, ed., Handbook of Terahertz Technology for Imaging, Sensing and Communications, WoodheadPublishing Series in Electronic and optical materials (Woodhead Publishing, 2013).
24. F. Tauser, C. Rausch, J. H. Posthumus, and F. Lison, "Electronically controlled optical sampling using 100 MHz repetition rate fiber lasers," in Commercial and Biomedical Applications of Ultrafast Lasers VIII (SPIE,2008), Vol. 6881, pp. 139–146.
25. T. Hochrein, R. Wilk, M. Mei, R. Holzwarth, N. Krumbholz, and M. Koch, "Optical sampling by laser cavitytuning," Opt. Express 18, 1613–1617 (2010).
26. M. Kolano, B. Gräf, S. Weber, D. Molter, and G. von Freymann, "Single-laser polarization-controlled optical sampling system for THz-TDS," Opt. Lett. 43, 1351–1354 (2018).
27. A. Bartels, R. Cerna, C. Kistner, A. Thoma, F. Hudert, C. Janke, and T. Dekorsy, "Ultrafast time-domain spectroscopy based on high-speed asynchronous optical sampling," Rev. Sci. Instrum. 78, 035107 (2007).
28. O. Kliebisch, D. C. Heinecke, and T. Dekorsy, "Ultrafast time-domain spectroscopy system using 10 GHz asynchronous optical sampling with 100 kHz scan rate," Opt. Express 24, 29930–29940 (2016).
29. S. Schilt, N. Bucalovic, V. Dolgovskiy, C. Schori, M. C. Stumpf, G. D. Domenico, S. Pekarek, A. E. H.Oehler, T. Südmeyer, U. Keller, and P. Thomann, "Fully stabilized optical frequency comb with sub-radian CEO phase noise from a SESAM-modelocked 1.5-µm solid-state laser," Opt. Express 19, 24171–24181
(2011).
30. A. Klenner, M. Golling, and U. Keller, "High peak power gigahertz Yb:CALGO laser," Opt. Express 22,11884–11891 (2014).
31. T. D. Shoji, W. Xie, K. L. Silverman, A. Feldman, T. Harvey, R. P. Mirin, and T. R. Schibli, "Ultra-low noise monolithic mode-locked solid-state laser," Optica 3, 995–998 (2016).
32. A. S. Mayer, C. R. Phillips, and U. Keller, "Watt-level 10-gigahertz solid-state laser enabled by self de focusing nonlinearities in an aperiodically poled crystal," Nat. Commun. 8, 1673 (2017).
33. S. Kimura, S. Tani, and Y. Kobayashi, "Kerr-lens mode locking above a 20 GHz repetition rate," Optica 6,532–533 (2019).
34. M. Hamrouni, F. Labaye, N. Modsching, V. J. Wittwer, and T. Südmeyer, "Efficient high-power sub-50-fs gigahertz repetition rate diode-pumped solid-state laser," Opt. Express 30, 30012–30019 (2022).
35. H. A. Haus and A. Mecozzi, "Noise of mode-locked lasers," IEEE J. Quantum Electron. 29, 983–996 (1993).36. R. Paschotta, A. Schlatter, S. C. Zeller, H. R. Telle, and U. Keller, "Optical phase noise and carrier-envelope offset noise of mode-locked lasers," Appl. Phys. B 82, 265–273 (2006).
37. S. M. Link, A. Klenner, M. Mangold, C. A. Zaugg, M. Golling, B. W. Tilma, and U. Keller, "Dual-comb modelocked laser," Opt. Express 23, 5521–5531 (2015).
38. T. Ideguchi, T. Nakamura, Y. Kobayashi, and K. Goda, "Kerr-lens mode-locked bidirectional dual-comb ring laser for broadband dual-comb spectroscopy," Optica 3, 748–753 (2016).
39. S. Mehravar, R. A. Norwood, N. Peyghambarian, and K. Kieu, "Real-time dual-comb spectroscopy with a free-running bidirectionally mode-locked fiber laser," Appl. Phys. Lett. 108, 231104 (2016).
40. B. Willenberg, B. Willenberg, J. Pupeikis, J. Pupeikis, L. M. Krüger, F. Koch, C. R. Phillips, and U. Keller,"Femtosecond dual-comb Yb:CaF2 laser from a single free-running polarization-multiplexed cavity foroptical sampling applications," Opt. Express 28, 30275–30288 (2020).
41. J. Pupeikis, B. Willenberg, F. Bruno, M. Hettich, A. Nussbaum-Lapping, M. Golling, C. P. Bauer, S. L.Camenzind, A. Benayad, P. Camy, B. Audoin, C. R. Phillips, and U. Keller, "Picosecond ultrasonics with a free-running dual-comb laser," Opt. Express 29, 35735–35754 (2021).
42. S. L. Camenzind, T. Sevim, B. Willenberg, J. Pupeikis, A. Nussbaum-Lapping, C. R. Phillips, and U. Keller,"Free-running Yb:KYW dual-comb oscillator in a MOPA architecture," Opt. Express 31, 6633–6648 (2023).
43. J. Pupeikis, B. Willenberg, S. L. Camenzind, A. Benayad, P. Camy, C. R. Phillips, and U. Keller, "Spatially multiplexed single-cavity dual-comb laser," Optica 9, 713–716 (2022).
44. C. R. Phillips, B. Willenberg, A. Nussbaum-Lapping, F. Callegari, S. L. Camenzind, J. Pupeikis, and U.Keller, "Coherently averaged dual-comb spectroscopy with a low-noise and high-power free-running gigahertz dual-comb laser," Opt. Express 31, 7103–7119 (2023).
45. J. Pupeikis, W. Hu, B. Willenberg, M. Mehendale, G. A. Antonelli, C. R. Phillips, and U. Keller, "Efficient pump-probe sampling with a single-cavity dual-comb laser: Application in ultrafast photoacoustics,"Photoacoustics 29, 100439 (2023).
46. S. L. Camenzind, D. Koenen, B. Willenberg, J. Pupeikis, C. R. Phillips, and U. Keller, "Timing jitter characterization of free-running dual-comb laser with sub-attosecond resolution using optical heterodyne detection," Opt. Express 30, 5075–5094 (2022).
47. R. V. Kochanov, I. E. Gordon, L. S. Rothman, P. Wcisło, C. Hill, and J. S. Wilzewski, "HITRAN Application Programming Interface (HAPI): A comprehensive approach to working with spectroscopic data," J. Quant. Spectrosc. Radiat. Transf. 177, 15–30 (2016).
48. S. Meninger, "Phase Noise and Jitter," in Clocking in Modern VLSI Systems, T. Xanthopoulos, ed., Integrated Circuits and Systems (Springer US, 2009), pp. 139–181.
49. B. Globisch, R. J. B. Dietz, R. B. Kohlhaas, T. Göbel, M. Schell, D. Alcer, M. Semtsiv, and W. T. Masselink,"Iron doped InGaAs: Competitive THz emitters and detectors fabricated from the same photoconductor," J.Appl. Phys. 121, 053102 (2017).
50. R. B. Kohlhaas, S. Breuer, S. Nellen, L. Liebermeister, M. Schell, M. P. Semtsiv, W. T. Masselink, and B.Globisch, "Photoconductive terahertz detectors with 105 dB peak dynamic range made of rhodium doped InGaAs," Appl. Phys. Lett. 114, 221103 (2019).
51. G. D. Domenico, S. Schilt, and P. Thomann, "Simple approach to the relation between laser frequency noise and laser line shape," Appl. Opt. 49, 4801–4807 (2010).
上一篇:扫描式荧光寿命成像技术简介
 上海市徐汇区虹梅路2007号6号楼43楼
上海市徐汇区虹梅路2007号6号楼43楼 [email protected]
[email protected]
昊量微信在线客服

昊量微信在线客服
版权所有 © 2024上海昊量光电设备有限公司 备案号:津ICP备55480275号 技术支持: Sitemap.xml