光子源偏振纠缠验证

光子源偏振纠缠验证实验

1900年，普朗克为了克服经典理论解释黑体辐射规律的困难，引入了能量子概念，为量子理论奠下了基石。随后，爱因斯坦针对光电效应实验与经典理论的矛盾，提出了光量子假说，并在固体比热问题上成功地运用了能量子概念，为量子理论的发展打开了局面。1913年，玻尔在卢瑟福有核模型的基础上运用量子化概念，对氢光谱作出了满意的解释，使量子论取得了初步胜利。从1900年到1913年，可以称为量子论的早期。以后，玻尔、索末菲和其他许多物理学家为发展量子理论花了很大力气，却遇到了严重困难。要从根本上解决问题，只有待于新的思想，那就是“波粒二象性"。光的波粒二象性早在1905年和1916年就已由爱因斯坦提出，并于1916年和1923年先后得到密立根光电效应实验和康普顿X射线散射实验证实，而物质粒子的波粒二象性却是晚至1923年才由德布罗意提出。这以后经过海森堡，薛定谔、玻恩和狄拉克等人的开创性工作，终于在1925年到1928年才形成完整的量子力学理论，与爱因斯坦相对论并肩形成现代物理学的两大理论支柱。

但针对于量子力学的完备性问题，爱因斯坦与波尔进行了十分长久的争论。1935年，爱因斯坦、波多尔斯基和罗森提出了EPR佯谬。定域实在论的提出，让众多科学家争论了数十年。1964年，贝尔不等式的提出，将这一理论上的问题转换到了实验中可验证的领域。引起了科学家们的广泛关注。为了验证贝尔不等式的正确性，众多科学家用不同的方法进行了实验，其中阿兰·阿斯佩、约翰·克劳泽、安东·塞林格三人贡献zui为突出，因此获得了于2022年获诺贝尔物理学奖，以表彰对纠缠光子实验、验证违反贝尔不等式和开创量子信息科学方面所做出的贡献。

为了验证贝尔不等式，人们渐渐的将目光转向了如何产生纠缠光子对这个问题上，经过数十年的发展，目前主要产生纠缠光子的方法主要有自发参量下转换与自发四波混频等。此处我们主要介绍自发参量下转化。

自发参量下转换过程，指的是一束高频光（泵浦光，pump）入射到非线性晶体上，产生两束低频光的现象，这两束低频光分别称为信号光(signal)和闲置光(idler)。当信号光和闲置光初始均处于真空态时，则称为自发参量下转换(SPDC)。

一般要求参量下转换过程满足所谓的位相匹配条件，即能量守恒条件和动量 守恒条件。我们用下标p、s、i分别表示泵浦光(pump)，信号光(signal)、闲置光(idler)，则能量守恒条件和动量守恒条件分别为:

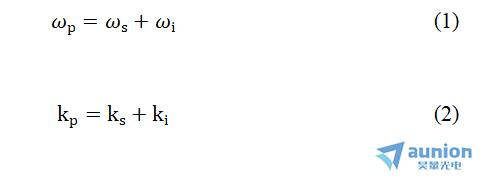
其中，w表示频率，k表示波矢量。

描述非简并参量下转换过程的相互作用哈密顿量为:

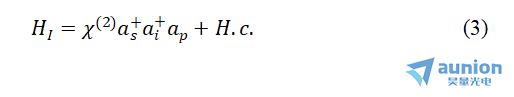
其中，χ(2)是二阶非线性极化率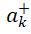；和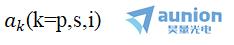分别表示k光的光子产生和湮灭算符。

一般来说，泵浦场较强，可作经典描述(称为参量近似),于是上式变为：

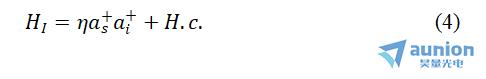
其中，η∝χ(2)Ep，Ep为泵浦光的振幅。

实际上，非简并自发参量下转换过程还分为两类。在第1类中，信号光和闲置光的偏振方向相同，且均与泵浦光的偏振方向垂直。在第二类中，信号光和闲置光的偏振方向垂直。下面分别予以讨论。

在第1类SPDC中，信号光和闲置光的偏振方向相同，其相互作用哈密顿量可由式(4)表示。由于位相匹配条件的要求，信号光和闲置光的传播方向分别位 于以泵浦光传播方向为轴的同心圆锥的不同两侧（在非简并情况下，信号光和闲置光位于不同圆锥；在简并情况下，信号光和闲置光位于相同圆锥），如图1和图2所示。

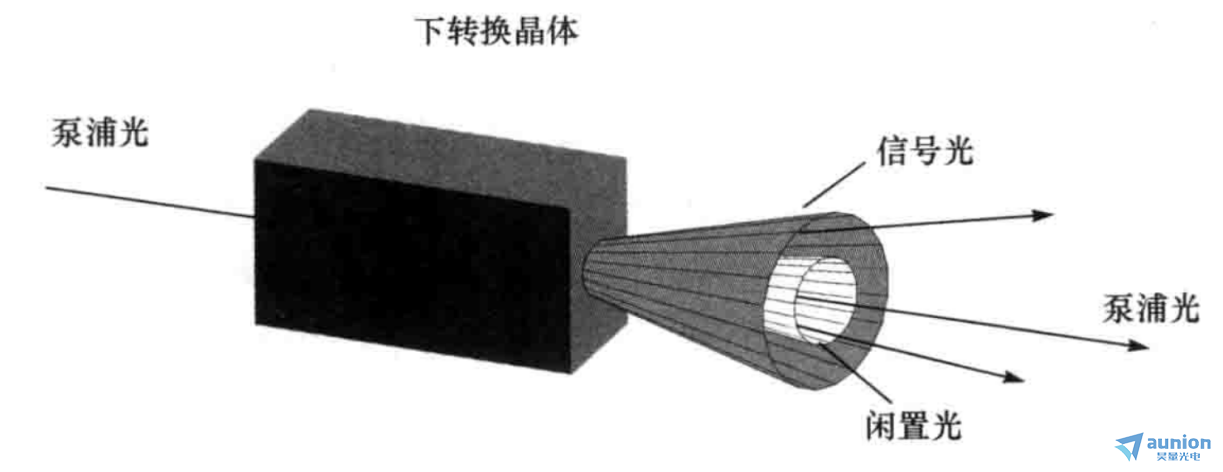
图1 第1类 SPDC光束示意图

显然，在满足位相匹配条件的要求下，有无穷多种方式选择信号光和闲置光的传播方向，几种光束截面，如图2所示。

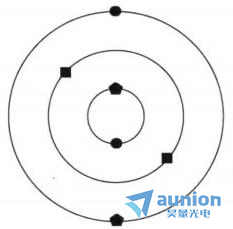
(a)光束截面(相同符号表示满足位相匹配条件的共轭光子，中间圆上的两个光子的频率是简并的)

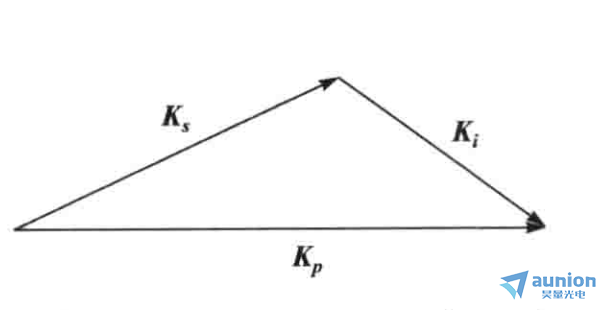
(b)位相匹配条件

图2 第1类SPDC 光束截面和位相匹配条件示意图

设信号光和闲置光初始处于状态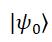，则t时刻的状态为：

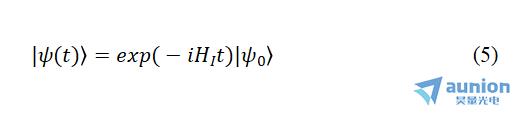
将指数展开，并取到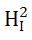项，得：

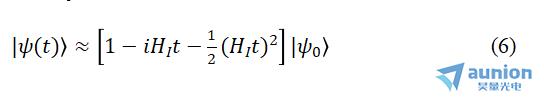
设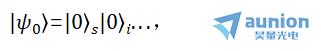

将其与式(4)代入式(6)可得：

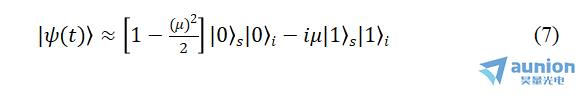
其中，μ=ηt，上式中略去了含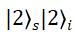的项。

上式是真空态和单光子态的纠缠态，可见利用第1类SPDC，可制备光子数态的纠缠态。

在第二类SPDC中，信号光和闲置光的偏振方向垂直。由于双折射效应，信号光和闲置光将沿不同心的圆锥传播，其中一束为正常波（o波），一束为异常波（e波），如图3所示。在圆锥截面的重叠处，信号光子和闲置光子处于偏振纠缠态，如图4所示。

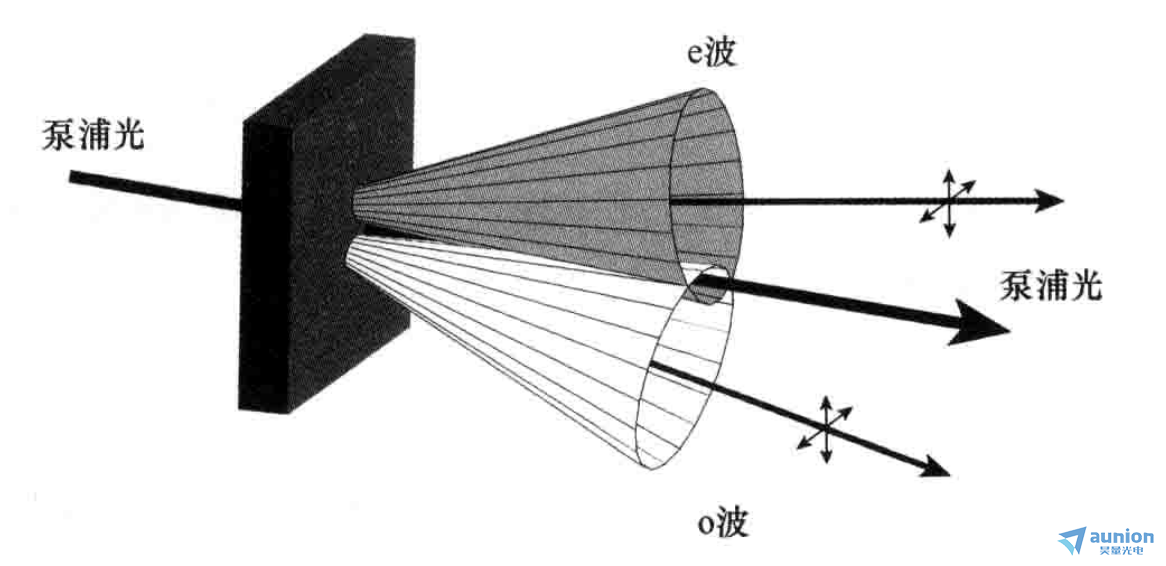
图3 第二类SPDC光束示意图

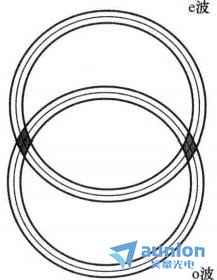
图4 第二类SPDC光束截面示意图

我们用H和V分别表示水平偏振和垂直偏振，则在参量近似下，描述第二类SPDC的相互作用哈密顿量为：

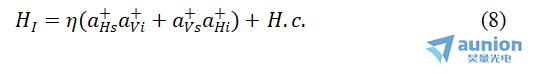
其中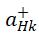，与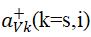(k=s,i)分别表示产生H和V偏振的k模光子的光子产生算符。

下面讨论量子态的时间演化，对第二类SPDC，式(5)和式(6)的形式仍然成立，不过要用式(8)的哈密顿量，信号光和闲置光的初态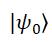也要作相应变化。设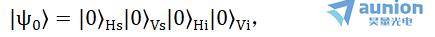，则利用式(6)和式(8)可得：

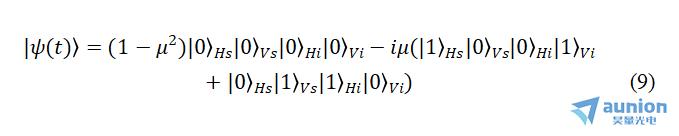
定义如下的偏振真空态和偏振单光子态，即：

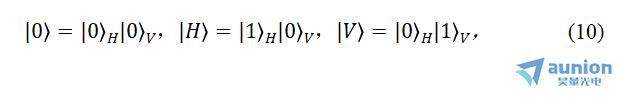
则式(9)可写为：

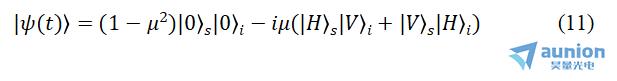
其中，第二项归一化后的形式为：

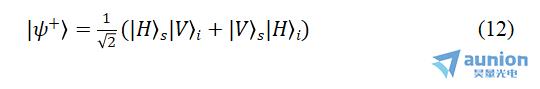
这是zui大纠缠的偏振纠缠态。可见，利用第二类SPDC，可制备单光子偏振纠缠态，或者说，可以产生偏振纠缠的光子对。

图5 纠缠光子源TPS 1550

昊量光电du家代理的独立量子纠缠光子源TPS 1550，由法国Aurea公司推出。这是一台高性能、紧凑且易于使用的独立双光子源，该纠缠源基于台式设计，将温度可调的ppln波导晶体与波长稳定的激光源结合在一起，可在室温下使用。其仅用5mW的泵浦功率，在C波段产生正交偏振的频率纠缠光子，光子数超过250000光子/秒。其在周期性极化铌酸锂ppln波导(准相位匹配-QPM)中，通过自发参量下转换(SPDC)产生纠缠光子对，是量子信息技术的理想选择。通过USB接口和专有软件接口控制激光泵浦功率和晶体内部温度，以高精度调整相位匹配。我们同时还提供DLL文件以方便您使用LabVIEW，C++，Visual basic等语言进行控制或二次开发。本次实验我们将验证其偏振性。

除了必要的光子源，我们还需要单光子探测器与高性能计数器。我们本次使用的是同样由该公司推出的NIR单光子探测器模块OEM，以及由Swabian公司推出的时间相关计数器 TimeTagger。

NIR单光子探测器模块OEM为900 nm至1700 nm近红外波段的单光子探测带来了重大突破。其基于冷却InGaAs/InP 盖革模式单光子雪崩光电二极管技术，可执行“门控"(GM)和“自由运行"(FR)探测模式。针对您的需求，该单光子探测器提供了标准版与guan军版两个版本。guan军版具有低至800 cps的超低噪声、高达30 %的高校准量子效率、100 nszui小死时间、100 MHz外部触发器、150 ps的快速分辨率和极低脉冲。标准级提供了非常有价值和成本效益的解决方案。SPD_OEM_NIR设计精良，结构紧凑，接口先jin，使用远程控制软件，提供Python、C++、LabVIEW的DLL，非常容易集成到要求苛刻的分析仪器和量子系统中。时间相关计数器 TimeTagger全系列分辨率为1ps，抖动zui低可达2ps，死时间可达1.5ns，zui多支持18通道，是您进行量子光学、激光雷达、荧光寿命成像、单光子源表征等领域的得力帮手。

图6 单光子探测器模块

图7 时间相关计数器 Time Tagger Ultra

纠缠源、探测器与计数器的页面如下图所示。纠缠源可通过仪器自带的触摸屏进行衰减、晶体温度、开关等设置，操作简便。也可通过usb线连接至PC，在PC端进行设置。单光子探测器可实时观察到当前实验环境温度与探测值，并可简便修改Count rate、dead time、效率、探测模式等，我们还可以设置输出信号参数形式，以数字信号、模拟信号、NIM进行输出。我们选择输出数字信号进入计数器。计数器中有众多预设，如“Counter time trace"、“Bidirectional Histogram"、“Logarithmic Histogram"等，可供不同应用需求进行选择。我们选用“Bidirectional Histogram"模式，并可对Bin宽，Bin数与采集方式等进行修改。

图8 纠缠源设置屏幕

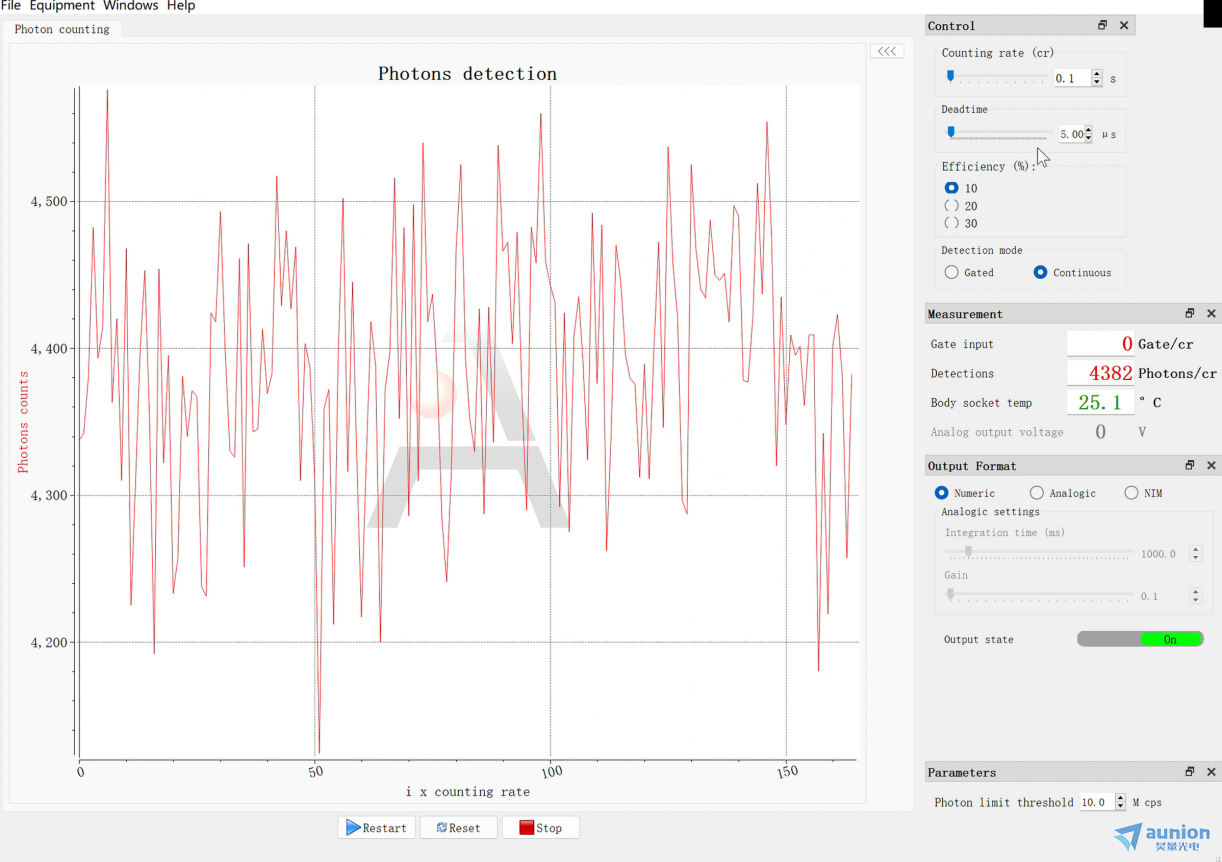
图9 探测器软件界面

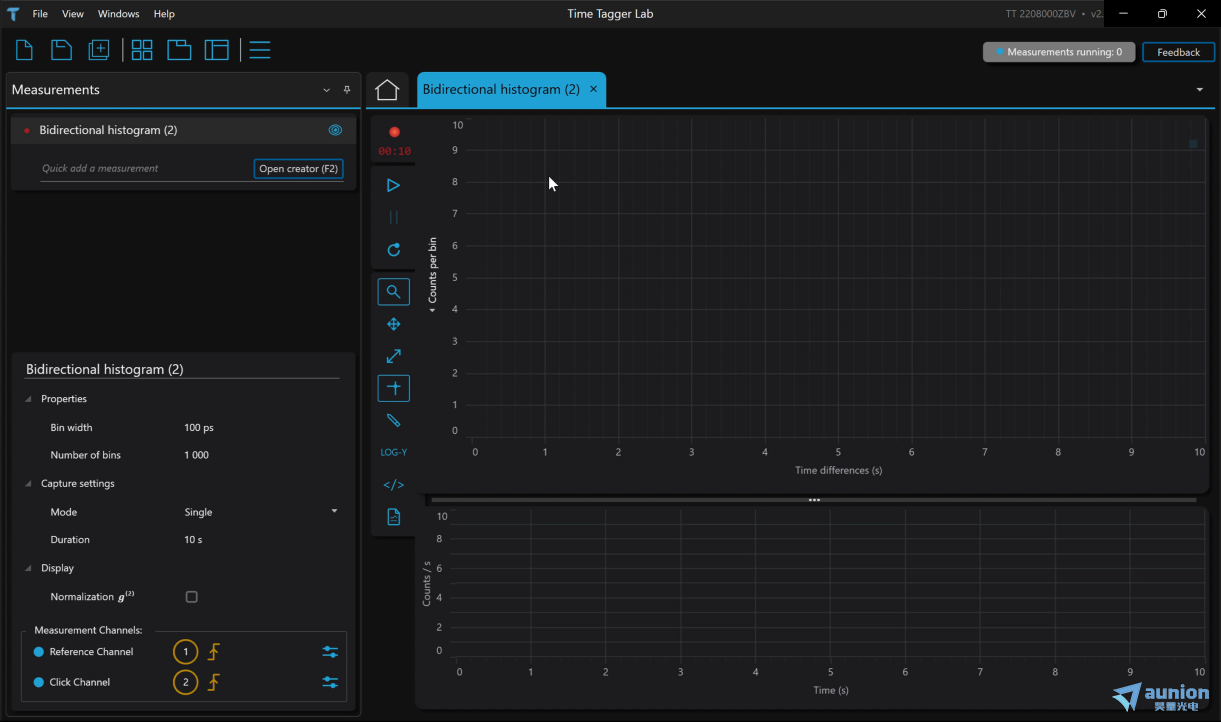
图10 计数器软件界面

本次实验中我们设置光子源的衰减为5dB，探测器死时间为20μs，计数器Bin宽为500ps，本次实验还需要1550nm激光器，1550nm准直器，偏振片，半波片与四分之一波片等。利用这些器材，我们就可以着手开始验证其产生光子对的偏振纠缠性。

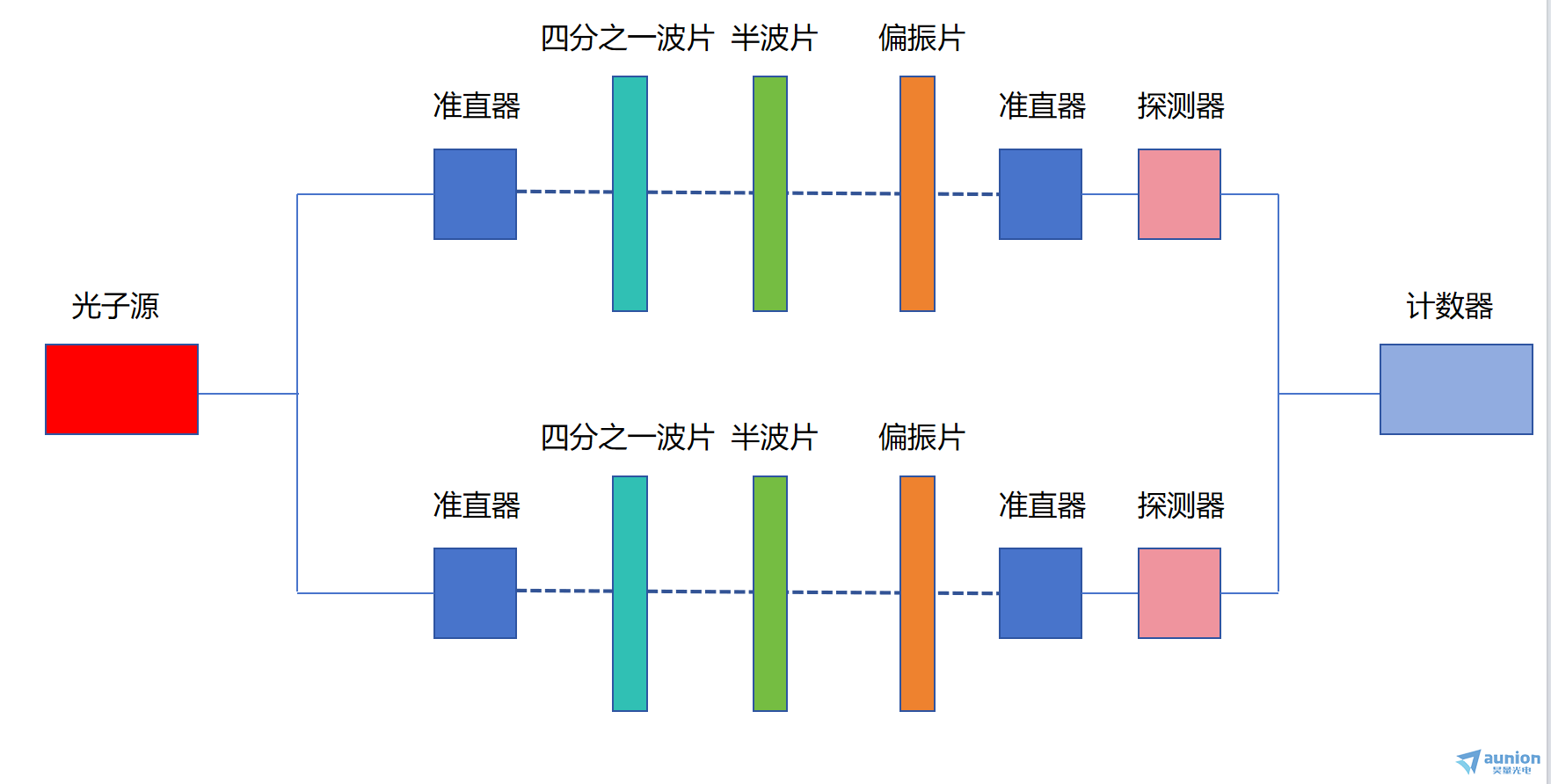
图11 验证光路示意图

图12 实际光路

我们搭建了如图所示的光路，我们首先使用可见光源与功率计将准直器对准。然后更换为1550nm偏振光源与功率计，分步加入偏振片、半波片与四分之一波片并调整角度，zui后更换为光子源，单光子探测器与计数器，光子源的信号光与闲置光将分别经过光纤，通过四分之一波片、半波片与偏振片，zui后由探测器探测，由计数器进行符合。我们保持光路光路其他波片固定，通过转动其中一个半波片并固定，我们可以在计数器中看到符合计数产生了变化。随着半波片的旋转，符合计数也随之发生正弦变化。

本次实验中，我们每次将旋转半波片5度，固定后在计数器中采集10s，我们将在此角度得到一个符合计数，再旋转半波片5度，重复上述步骤，我们可得到半波片不同角度下的符合计数。将符合计数记录后进行拟合，具体可见图，其中蓝色线为可得到一正弦变化的曲线，其中散点为测试所得数据，黄色线为拟合正弦曲线。我们可以看出，所得数据点非常符合正弦曲线趋势。zui高值与zui低值相差为45°，其中zui高值为818，zui低值为14，对比度约为98.2%，超过95%，证明了其偏振纠缠性。

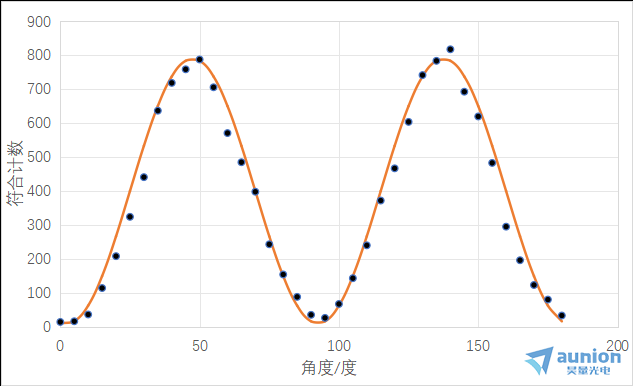
图13 符合计数随角度呈正弦变化

通过本次实验，我们使用了1550nm波长的相关光学器件、Aurea的单光子探测器与Swabian的1ps时间分辨率计数器，计算出TPS1550单光子纠缠源的对比度可达98.2%，证明了其偏振纠缠性。

参考文献：

[1] 物理学史[M]

[2] 量子光学[M]

更多详情请联系昊量光电/欢迎直接联系昊量光电

关于昊量光电：

上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。